Appreciating Randomness...E.coli Interupted

[mycrap]
Presenting a classic problem in genetics...a great way to introduce oneself to Mr. Poisson (of the distribution fame)...the joy of modelling...
[/mycrap]

Problem: The transfer of DNA from Hfr begins at oriT. The gene closest to oriT on the donor chromosome enters the recepient cell, followed by successive genes on the donor chromosome. The frequency of a particular gene entering the recepient is a function of its distance from oriT. Moreover, this frequency is found to decrease "exponentially" with a gene's distance from oriT. Why is this decrease exponential (and not linear, say)?

The Solution:
Poisson says

"Let m = the mean number of successful events. The probability of k successful events is given by the formula -
P(k) = (e^-m * m^k) / k!"

The key to solving the given problem is to define the 'm' value. Let us define the m value as the 'number of breaks per unit length of the chromosome'. So if 'x' is the length of a given chromosome segment the number of breaks in x will equal 'mx'. Remember that mx is the average number of breaks in a population of chromosome segments of length x. That is some x-lengthers will have more that mx breaks and some less than mx and some may even have zero breaks.

Even a single break in a length x is sufficient to ensure that a marker at distance x from oriT is not transferred. In other words any non-zero number of breaks in x will prevent marker at x from being transferred.

Now consider a circular ds DNA E.coli chromosome. Consider markers located at distances x1, x2 and x3 respectively from oriT.



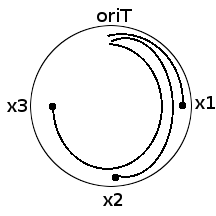
What are we distributing? Good question. We are distributing 'breaks' to x-length chromosome segment populations.






In case of x1-lengthers,
P(0) = Probability of having 0-break x1-lengthers = e^-mx1
P(1) = Probability of having 1-break x1-lengthers = mx1 * e^-mx1
P(2) = Probability of having 2-break x1-lengthers = (mx1^2 * e^-mx1) / 2
P(3) = Probability of having 3-break x1-lengthers = (mx1^3 * e^-mx1) / 6
.
.
.

Now comes the good part..

We are interested in whether a marker within distance x is transferred. It will be transferred if there are zero breaks in the length x. Hence we are interested in the fraction of those x-lengthers which have zero breaks. We are interested in the zero term P(0).
P(0) = e^-mx1

Similarly, fraction of markers at x2 transferred to the recepient,
P(0) = e^-mx2 and
fraction of markers at x3 transferred to the recepient,
P(0) = e^-mx3.

If we plot the values of P(0) for x1-lengthers, x2-lengthers and x3-lengthers versus the distance x1, x2, x3 then obvioulsy an exponentially decaying curve would be obtained. Multiplying the P(0) values of each by the total colonies scored will give the expected number of colonies recombinant for these markers, decaying exponentially with each's distance from oriT.